|
Different uses for voting
need different types of voting. |
 |
MMVa Tally Steps |
 |

|
|
|
Overview of the Tally:For Movable Money Votes, each voter's share of the fair-share fund is that individual's account, so it rewards efficient use. The voter rates each item and, within limits, may change their recommended budgets. A voter’s ballot offers each of his favorites some of his share. A full offer to an item equals his favored budget divided by the quota of offers it must win. For example, if the voter’s budget for P is $300 and the quota is 10 offers, one offer will be $30. That offer gives the item one vote. (This combines the two measures of popularity, money and votes, into one. It is the key for adapting STV to selecting projects.) If P gets its quota of 10 offers, those offers become real contributions. The item's final budget will equal this total amount contributed to it. Its total contributions equal the average of its supporters’ favored budgets, weighted by how many votes each gave. (It is just as if those budgets had been totaled and then divided by the quota). Thus the quota of offers combines a number of supporters and the item's final budget. These prove the intensity and breadth of support, to pay for the item and qualify it as a public good. The minimum suggested budget for a project is set by the project's sponsor. The quota of offers is set in the council’s by-laws. A voter’s ballot offers money to its top-ranked items, as many as his share can afford. The tally suspends and transfers offers from the weakest items one at a time. It also transfers excess offers until all remaining items have exactly a quota, just as STV transfers excess votes.
Fair Share Voting advanced (FSVa)Again we compare MMV to problems in old funding rules, to the Single Transferable Vote (STV) process for elections, and to goals for Fair Share Voting rules. The goals for spending rules are tougher than those for elections. Each feature of MMVA is simple. But the features work together; thus you cannot fully understand one until you see how it works with the others. That discussion follows this list of features. Candidates
Ballot
MMVA lets each voter say both B) how useful an item is and B$) how much money it should get. Voting is easy. Quota
Weight
Eliminations and Transfers
Offers ****
DiscussionMinimum Budgets prevent an opponent from dragging down the budget of a sure winner by giving it an unworkable low budget. To damage an item's budget, opponents would have to give up a significant part of their shares. And by giving a sure winner excess votes, its opponents would help their rivals keep money to spend on other goods. Minimum budgets also prevent half-hearted support from counting toward quota. Without out this, strategists could conspire to let each other fund private goods in this way: A quota of voters would agree to give $1 to each others' projects so they all qualify as public goods. Each sponsor would make her own favored budget equal to quota times the true price. Thus she would "pay" the full budget -- but she would be spending public funds on her private good. Setting a narrow range of budgets prevents this strategy. Maximum budgets limit exaggerated favored budgets. Exaggeration does help raise the item's final budget -- but at the cost of a large contribution and reduced offers to other items. A voter may feel it is worth that cost to help increase the budget of a favorite. (Using the median vote instead of the mean average would make that ineffective -- but would break the logic of voters paying for projects' budgets.) Thirty years experience at one organization shows the largest group of voters stick with the suggested budgets. Very few give the maximum but many voters give the minimum so they can help more items win. Quota A quota of offers actually combines 2 quotas: a minimum number of supporters and the item's cost. The item must fill both quotas. The cost quota must be filled to prove the intensity of support. The quota of ballots must be filled to prove the item's breadth of support. The philosophy is that a number of people is required to qualify an item as a public good.
Equity Process In MMVA: Ballot WeightsEach voter may start with an equal share of the budget or shares may vary based on contributions to the organization.(MMVA takes its total budget as an external given. It was developed for an organization that gives some of the coming year's projected surplus to a discretionary fund. Asked whether we should let voters add personal money to their voting weight, thus increasing the budget, their personal "tax" and their influence on the public goods selected, they laughed, "No one would do that; we all want our personal funds for personal uses." Civic clubs and religious groups might choose voluntary donations. )
Utility Process In MMVA: Variable VotesMMVA tries to maximize the "utility value" or happiness per dollar. A ballot's average offer gets 1 vote, but its highest priorities get more than 1 and its lower offers will get less than 1 vote each. It still offers money to as many top items as it could afford to if it were offering 1 vote to each.G) If a voter scores item A twice as high as B, A gets twice as many votes. G$) A ballot must pay for each vote. A ballot pays for 2 votes by offering 2 × FB / Quota. A voter just marks ranks or scores on a ballot, and Favored Budgets for proposals that are variable. H) If quota were 15 and a voter could give 15 votes to 1 item, the votes would not measure public good. So to prevent "bullet" voting the by-laws set a maximum on the votes a ballot may give an item. I) If a ballot has some money, but less than the cost of a full offer for its next favorite item, it makes a partial offer and gives a partial vote.
Utility and Equity: Power Points ****A ballot offers both votes and money to as many items as it could afford if it gave 1 vote, 1 offer, to each. With the exception of partial votes as noted above, if you add up a ballot's offer A + offer B, etc. you'll find they equal 1 weight. [This is somewhat arbitrary; it could be a variable. But changing this has the same affect as changing the quota: it makes each ballot concentrate its share on a few items or spread its funds more thinly. Rather than have two variables with the same affect, we will vary only the quota.]A ranked ballot puts the voter's favorites in order under a utility curve. A scored ballot doesn't give 1 vote to each of these favorites. It makes their votes proportional to the voter's scores; some >1 some <1. Thus items with high scores are more likely to win. On a scored ballot, the only important things to the voter and to the tally are the ratios between items. It is widely known that the best strategy for most point voting is to dump all of one's points on one's favorite. This is bad for decision making. It is not an accurate or sincere rating. It doesn't tell the community or the vote-counting rule how one feels about all of the other items. It rewards exaggeration. Raw scores are never comparable between voters, even when they use the same scale. We can't know if Joe's use of points honestly has the same interpersonal value as Jane's. Scores will be adjusted so each ballot gives its fair share of power points: That is 1 vote × 1 share of money. The adjusted scores are comparable because every voter has the same power over FS funds. (We set aside the fact that private wealth often makes public funds and public goods less important to rich voters.)
Examples of Scored Ballots — optionalAn offer is multiplied by a number of votes; that is how many of those offers the ballot gives the item. Each ballot's (votes for A × offer A) + (votes for B × offer B) also add up to its weight; they must because that is all the money the ballot has. The following examples demonstrate this.These examples use simple fractions for easy multiplication. A real tally allows decimals. And the voters don't do any of this multiplication. Voters simply mark scores while thinking, "Is a hot tub really more fun per dollar than a sauna?"
Ten ballots like this can fund the item:
Ballot 2, Bobby can give a half vote offer for an item that costs twice his share of money. 1/2 × 2 = 1. It would take 20 such ballots to reach a quota of 10 full offers for this costly item:
If he can't quite afford that third item, it gets a partial vote. Let's say its Suggested Budget equals 10 shares, so one offer for it would equal one share, his ballot would offer
| ||||||||||||||||||||||
|
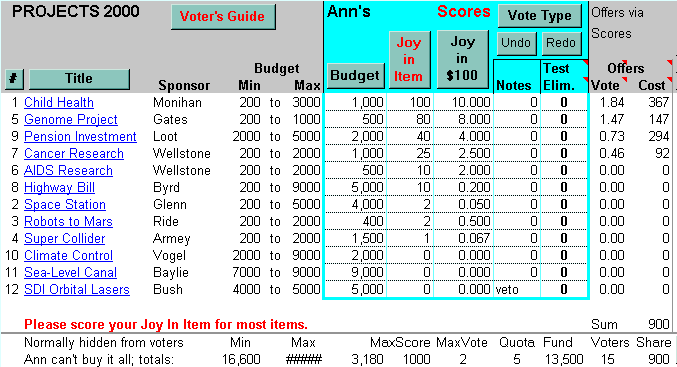
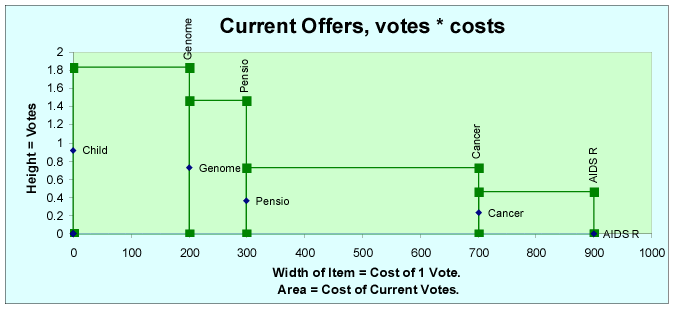
This graph, from the interactive ballot, shows a ballot's current offers. The height of an item's line shows the votes for it. The width of an item's line shows this voter's cost of 1 “offer” for 1 vote. The area under an item's line shows how much money the ballot currently offers the item; that is the item's votes times its cost for each vote.
→ Preset utility functions are simple lines. They cannot give a bumpy utility chart like this.
Steps to Calculate Votes from Scores — optionalHere are the main calculations for a scored ballot. (This does not show the calculations needed to group items with tied scores, nor to release each winner's excess percentage of votes to the ballot's other choices.)1) Use the sponsor's Suggested Budget or the voter's Favored Budget (FB) [adjusted for excess votes] to calculate the costs of 1 offer to his first choice A, 1 for second choice B, etc. Offer for First choice = FB for First choice / Quota, Offer for Second choice = FB for Second choice / Quota. 2) Make a running total of costs for favorite items to find how many items the ballot can afford. First, First+Second, First+Second+Third, and so on. 3) Calculate the fraction of an offer and vote available for the last affordable item. Partial vote = Item's cost / Remainder of share 4) Calculate score × cost for each affordable item then total those Raw Points. Score for First × Cost for 1 offer to First + the same for Second, + Third, and so on. 5) Adjust the Raw points for each item so the ballot's Total points equal the ballot's Money. The formula is: Adjusted points for First = Raw points for First × (Money / Total raw points) Likewise for the other affordable favorites. 6) Find the ballot's vote for an item by dividing its adjusted points by its cost. Adjusted points / Cost [NOT adjusted for excess votes] For each item, total the votes from all ballots. If an item gets more than quota, find its percentage of excess. On the next tally of ballots, reduce the item’s cost by that percentage. A ballot then can afford more items in step 2. Step 6 the full cost is used, thus the vote is reduced by the percentage of excess. This way, if an item gets more than a quota of votes, the excess offers stay with each ballot and move other favorites on the ballot. |

Review MMV Advanced | |
| Goal | Method |
| Fairness in money | One voter cannot spend another's share. |
|
Equality in money (optional) | Each voter spends an equal amount. Each voter's $ Account = Total $ / the number of Voters. |
| Reward frugality | Each voter has a limited amount to spend. |
| Intensely supported
as highly useful changed → | A voter rates each item's value. His ballot then gives 0 to [2] votes to each item. The ballot pays for each vote. One vote's Cost = Voter's Favored Budget / Quota A project's Final Budget = Total paid for votes. |
|
Broadly supported as a public good | Require a number of votes with money for a win and Limit the number of votes a ballot may give an item. |
| Equal power (optional) | A ballot’s Total (Votes × Costs) = the voter's $ Account. All ballots give equal Votes × Costs, if accounts are equal. |
| Resist Voting Strategies | |
| Exaggeration
| Set a maximum Favored Budget for each item.
Limit the number of votes a ballot may give to 1 item. |
| Free riding
changed → | Fund Condorcet winners before MMVA.
Use Meek's or Warren's vote-transfer rules. |
| Decapitation | Ineffective with Condorcet rules. |
| Divide And Conquer. | Ineffective with Condorcet or transferable-vote rules. |

|
|

 Accurate Democracy
Accurate Democracy