|
Different uses for voting
need different types of voting. |
 |
Tally Rules for
|
 |

 Equity factor: weights
Equity factor: weights Utility factor: variable votes
Utility factor: variable votes
|
 Review
Review
 Simplest program, Sim
Simplest program, Sim Improving a set of winners
Improving a set of winners |
|
Fair Share Budgets from Single Transferable VotesThe simplest case is when all projects have nearly the same cost(1) and each voter's share of money can pay for just a small fraction of a project. So it takes a large number and fraction of the voters to fund one project. Then most versions of Single Transferable Vote can give a good tally.But when projects vary in cost, a vote for a costly project should cost the voter more of his “weight” . And when a tiny number or fraction of the voters have enough money to fund a project, then we need a tally that does something more. We need to limit the fraction of a project's cost that a voter is allowed to pay — so a project needs to earn votes from a significant number or fraction of the voters. What is a significant number or fraction of the voters? That is up to each organization or jurisdiction. If 3% is 200 voters, that might be enough. But if 3% is just 3 voters, or if 200 voters is just a half a percent, that probably is not enough of a mandate for public funding. (1) Plus or minus one-third. More costly projects could be funded in parts, but this chapter has better voting methods for varied budgets. Some STV elections tally the ballots by hand. For a computer tally, the Tools page has free software. Meek's STV and Sequential STV are worth considering. Movable Money Votes Using CardsNote: This method of Fair Share Voting is easy to visualize, because it grows from the simple Movable-Vote Workshop. It has been superseded by a newer method developed by Robert Tupelo-Schneck and used by Twin Oaks Community. Comparing MMV with STVLet's compare a basic Movable Money Vote rule (MMV) to problems in old funding rules, to the Single Transferable Vote (STV) process for elections, and to goals for Fair Share Voting (FS). The goals for spending rules are tougher than those for elections. A discussion follows this list of the tally's features: Proposals and Candidates
Many voters want to know the expected costs for all projects before ranking them. Ballot
Quota
MMV quotas actually combine 2 quotas: a minimum number of supporters and the item's cost. The item must fill both quotas. The cost quota must be filled to prove the intensity of support. The quota of ballots must be filled to prove the item's breadth of support. One MMV workshop presents it this way:
As in Proportional Representation, the quota should be less than a majority. The council’s by-laws may set the quota, or a budget commitee may reset it every year. (An organization whose charter, constitution, or by-laws require majority support for allocations can use MMV in a survey, or by turning into a “committee of the whole” to vote, tally and report its result for adoption by the usual rules.) C$) MMV also requires an item to win its budget in contributions. This proves the supporters think it is worth its cost. Weight
Under STV a voter usually helps elect just one rep. Under MMV a low-cost item might cost its supporters only a little of their weights. So a voter can help fund several items. Eliminations and Transfers
DiscussionThirty years experience at one organization shows most voters stay close to most of the recommended budgets. And increases by some voters usually balance decreases by others. When that pattern became obvious, many people stopped voting, “Why bother”, they said. Still the community council likes the process as a way of teaching members and collecting polite feedback. Equity Process In MMV: Ballot WeightsThe process above has several variations.Each voter may start with an equal share of the budget, or shares may vary based on each voter's contributions to the organization or on the decision's impact on each voter. ( MMV takes its total budget as an external given. It was developed for an organization that puts some of the coming year's projected surplus into a discretionary fund. Asked whether we should let voters add personal money to their voting weight, thus increasing the budget, their personal “tax” and their influence on the public goods selected, some members laughed, “No one would do that; we all want our personal funds for personal use.” However, civic clubs and religious groups might choose voluntary donations. ) Utility Process In MMV: Variable VotesMMV tries to maximize the “utility value” or happiness per dollar. The tally can use several options to optimize this value. A ballot's average offer gets one vote, but its highest priorities may get more than one and its lower offers get less than one vote each. It still spreads its offers of money to as many top items as it could afford to if it were offering one vote to each. |
| Review Basic MMV | |
| Goal | Method |
| Fairness in money | One voter cannot spend another's share. |
|
Equality in money (optional) | Each voter spends an equal amount.
Each voter's $ Account = Total $ / the number of Voters. |
| Reward frugality | Each voter has a limited amount to spend. |
| Intensely supported
as highly useful . (optional) | A voter ranks or grades each item's value.
The ballot pays for each vote. The Cost of one vote = Proposed Budget / Quota A ballot may give 0 to 2 votes to each item. |
|
Broadly supported as a public good | Require a number of votes with money for a win and
Limit the number of votes a ballot may give an item. |
| Equal power (optional) | A ballot’s Total (Votes × Costs) = the voter's $ Account. All ballots give equal Votes × Costs, if accounts are equal. |
| Resist Common Voting Strategies | |
| Exaggeration
. | Set a Proposed Budget for each item.
Limit the number of votes a ballot may give to one item. |
| Free riding
. . | Fund Condorcet winners before MMV. 
Restart after each elimination. This prevents a voter from shielding cards under a first-ranked loser. |
| Decapitation | Ineffective with Condorcet rules. |
| Divide And Conquer. | Ineffective with Condorcet or transferable-vote rules. |
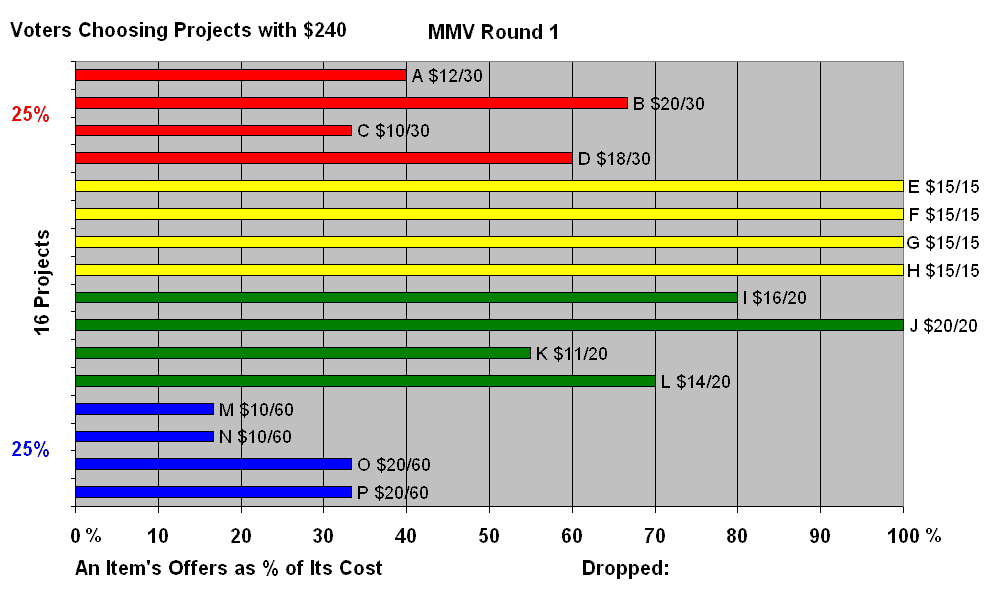
A Simple Tally MethodThis builds on the tally board used in the workshop on movable votes. Thumbnail: A spending tally gives each ballot 99 cards.
After all the cards are given, the item furthest from winning is excluded. That is the one with the lowest percentage of its cost. (Splitting an item into small pieces could keep each piece from being the item needing the most dollars.)
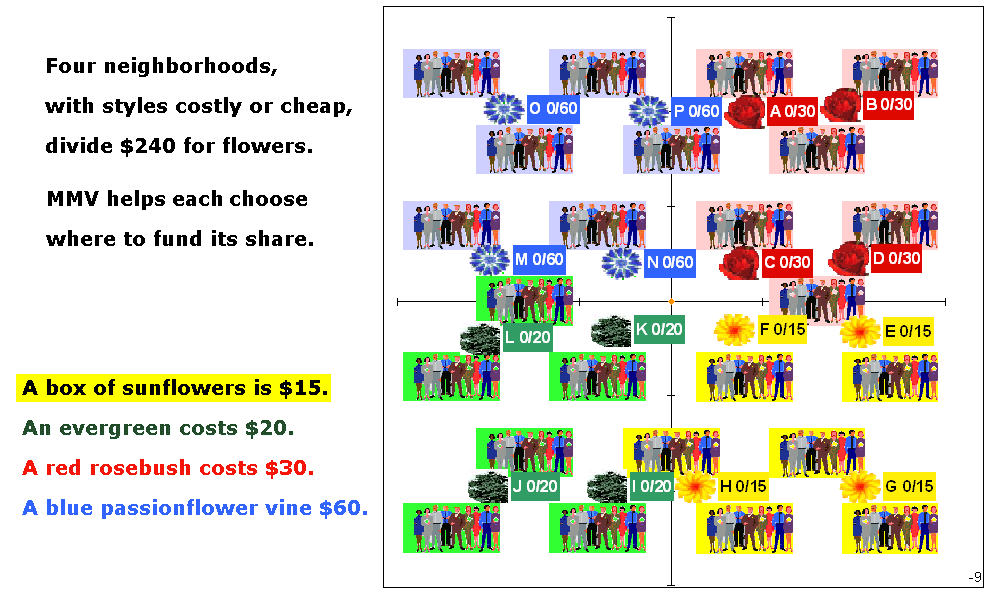
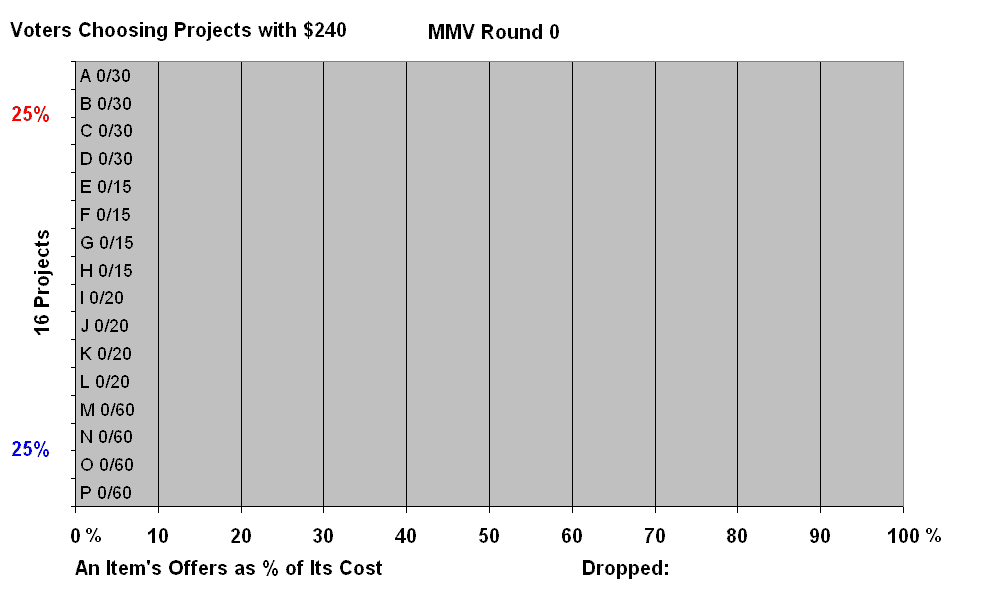
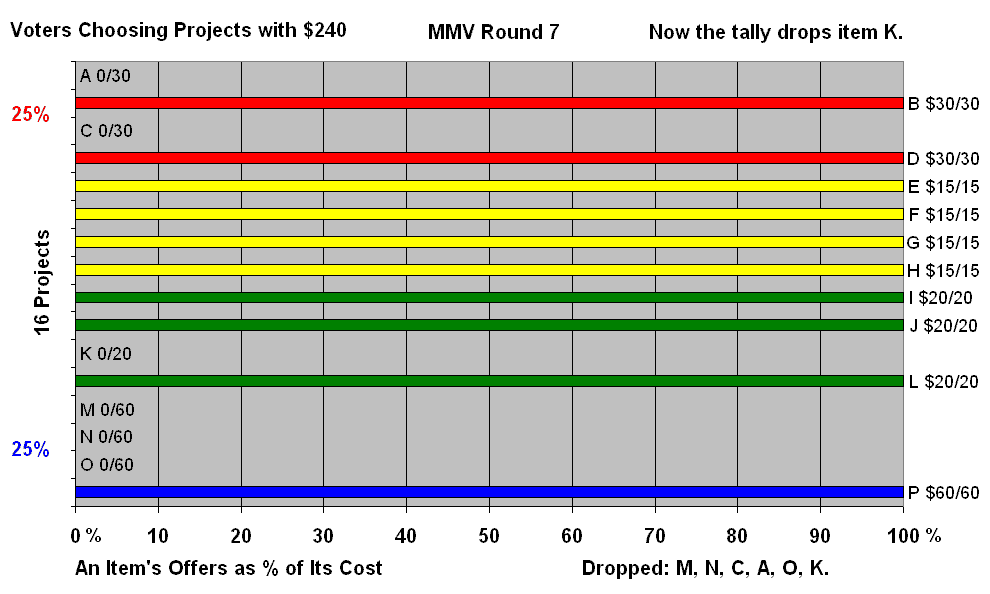
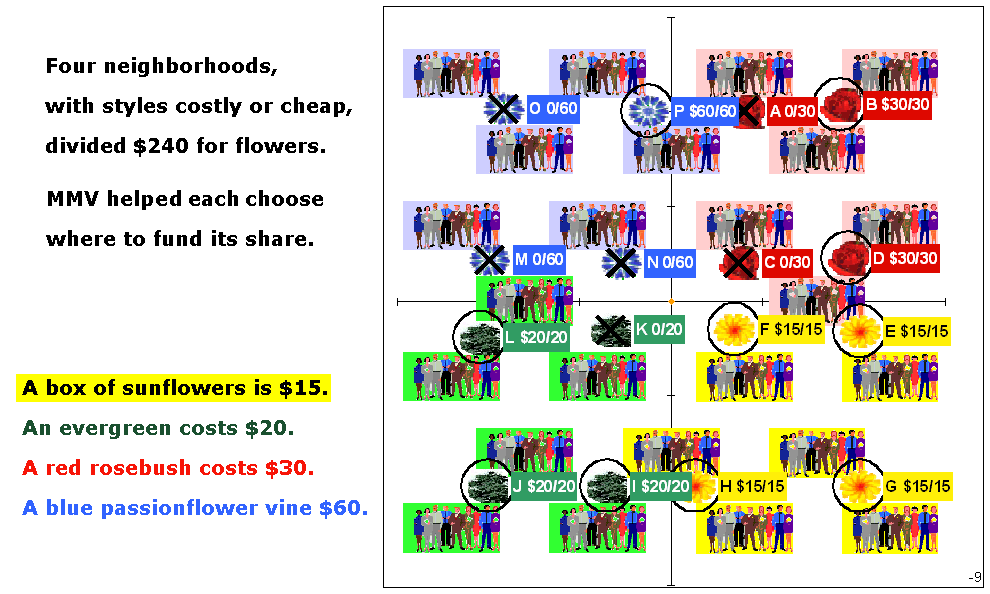
Those steps repeat until all of the remaining items are fully paid for; then the tally is complete. (Groups may decide to use a topping-up fund to fill up any item within $X or X% of its price.) Let's say each voter's ballot gets 99 cards that range in size from 198 down to 2; their average value is 100. These numbers could be pennies, yen, euros, labor hours, gallons, liters, exhibit space or another limiting resource. Drop1Loop, the outer most loop, drops the weakest item. If all remaining items are fully funded, it calls the ReportWriter. If not, it calls the CardLoop. CardLoop will loop once for each card, 99 times in this example. It selects the card that each ballot will offer on this loop, starting with the biggest card on the first loop. Then the CardLoop calls the BallotLoop. BallotLoop calls each ballot once. A ballot offers the selected card to the next column in the ballot's list of favorites. A ballot remembers how many cards (not dollars) it has given to each item. A ballot also can see how many columns an item has and limits itself to giving the item that number of cards, one per turn. If the item is fully funded, the ballot tries to give the card to the voter's next choice. A low-cost item is not eligible to receive cards if the current card is worth more than double the item's Cost / Quota. That is two votes. This keeps the quota real to prevent a small group of voters from funding a private item. The inexpensive item's single column can fill up quickly as soon as smaller cards come into play. Identical ballots have almost equal chances for offering cards to a favorite. The first ballot called by BallotLoop might give one more card to an item than the last ballot called, if some of the other ballots fill all the item’s columns during that BallotLoop. The difference of one card is not important if each ballot has many cards. By adding one small card at a time and stopping at the finish line, there are never significant “excess votes” to transfer. By restarting the Drop1Loop with all remaining candidates at zero after dropping each loser, a voter can't withhold some cards from sure winners during the earliest rounds by ranking a likely loser above the sure winners. Voters who sincerely rank losers high also pay their fair shares for their favorite winners. This approximates Brian Meek’s method to repeatedly adjust transfers of votes from winners. This tally logic uses whole numbers and could be done physically with real cards — if voters were willing to spend many hours as they each take turns to place one card at a time until all cards were used, drop the weakest, remove all cards from the board, and repeat taking turns to place one card at a time. This physical analogy helps voters visualize the logic and welcome a computer's help with the tally. A simulation of Fair Share Voting is free to download. It shows voters and proposed projects on a map. The example below has four equal-size groups that want different kinds of plants. The tally helps all voters organizes into interest groups, able to fund their favorite plants and in their favorite locations. Each group gets a fair share, $60, even though the prices vary. In real voting the interest groups are less distinct which makes MMV more essential for finding a fair solution. |





|
The results for the community are much better than winner take all. But the results for an individual might sometimes look illogical. Say you prefer A > B > C > D... then A, B, and C each win. Your personal result might show that your ballot contributes to A and C but nothing to B. It can happen this way: While you give big cards to A, other voters give big cards to B. They pay B's full cost before A is paid up — before your ballot would have started to give its smaller cards to B. The same pattern occurs in STV elections but is less noticeable. In a very simple case, you prefer A1 > A2 > B > C > D. B wins. A1 is eliminated. Then A2 wins with many extra votes. Your share of the extra helps elect C. Meek's STV solves that, and it has been adapted to Fair Share Voting. That is explained on the MMVa tally page. Robert Tupelo-Schneck made Meek-style STV the basis for his Fair Share Voting method. It is available in the open-source program OpenMMV. ]
Improving a Set of WinnersAfter the last elimination there are usually some voters with leftover money. We can reinstate the losers which cost less than or equal to the leftover money and continue the elimination process.It is also important to find popular items eliminated early. Such an item has broad but not intense appeal. It lacks top ranks on a quota of ballots, so it is eliminated before the good ranks it earned on many ballots would give it funding. Here are several ways to find and fund such items. The relatively simple “card” tally above may use techniques proposed to optimize sets of winners from Single Transferable Vote. The most common process is reinstating one loser at a time to test its popularity compared to each and every winner -- which Nicholas Tideman suggests is a shortcut to approximate his Comparison of Pairs of Outcomes by Single Transferable Vote (CPO-STV). I.D. Hill and Simon Gazeley have published a refined method for reinstating one at a time as “Sequential STV - a further modification.” And James Green-Armytage has also contributed in “Computational Conservation in CPO-STV.” But those methods are for STV elections where every candidate has the same set price in votes, and every ballot tries to give its full weight to its current top candidate. In Fair Share Voting the items can have a (wide) range of prices. So a tally cannot substitute one item for another of a different price. We want to select items needing different voting weights from supporters. Sticky ItemsThe last item eliminated from a set of proposals almost but never quite reaches quota. It lost despite an excellent chance to win when most other items already had been eliminated. It might be called a “sticky item” because it holds on to some of your money until your other high-rated items are funded or eliminated. You may be left with unspent money or see some go to a much lower choice because your middle choices have been eliminated. Either result hurts you. (MMVa will introduce suspension instead of elimination. )Delete Last LoserThe best practical optimization is probably Delete Last Loser.We want to give other items a better chance to use money offered to sticky items. Release the offers for the last loser by pre-eliminating it. Tally again. This may be repeated for several rounds, increasing the number of items pre-eliminated. Deleting the last loser can help an “exhausted” ballot, one which has money but no more favorites in the running, to distribute more of its money by giving more to each of its ‘tally A’ winners, and perhaps by helping new winners. By giving more, the ballot helps other voters who support those winners, saving them money for their lower preferences. These other voters likely have similar goals. When a last loser is eliminated or suspended, its money is available, at long last, for offers to items ranked below it on a ballot. Pre-eliminate the last losers one at a time to remove sticky items. Deleting last losers one at a time and running the entire elimination tally many times obviously takes time. But it is not expensive. Both delete last losers and reinstating one at a time are powerful tools for Fair Share Voting. The resulting sets of winner will be usually be very similar. Experience will teach us which method is more fair to interest groups or better at funding favorites. All forms of MMV are much more fair and efficient than old, winner-take-all rules. The rules should specify what to do with any leftover money. It can be put in investment, endowment, or emergency funds, given to all voters in the next allocation, or to other politically neutral uses.
We might improve MMV by giving each voter more cards, the same total value but with a smaller average value. The “utility curve” inherent in the set of cards becomes smoother. (Math savvy readers will see this is a step toward calculus. A later page shows how a ballot could use calculus to give voters a range of perfectly smooth utility curves. But the benefits are probably small and the complications large for those who must program or explain that ballot and tally.) The basic MMV on this page is good enough for most groups. In selecting projects as in electing reps, the difference between winner-take-all rules and fair-share rules is far greater than the differences among the fair-share rules. Voting in most situations can be improved and that is most evident in funding rules. This page has explained the logic and arithmetic of basic Movable Money Votes. Later pages explore the Loring Allocation Rule and optional features for MMV. The basic method is clear. But we're still experimenting with ways to optimize a tally. Sorry to say, some pages still show the creative disorder that often occurs during research and development. Free software in p_tools.htm gives a feel for grading, quotas, and varied budgets. Download and play with the simple simulation game. Microsoft Excel 5 or higher is required. Next, look at some ballots for Fair Share Voting |

|
|



 Accurate Democracy
Accurate Democracy